Introduction
At its core, modular arithmetic is a unique form of arithmetic intricately connected to remainders. The arithmetic operations within this system are based on the residual values left when integers are divided by a fixed quantity, known as the modulus. In simpler terms, modular arithmetic encapsulates the essence of counting within a cyclic framework, where the remainder after division becomes a central focus.
The roots of modular arithmetic extend back to ancient civilizations, where early mathematicians grappled with the cyclical nature of time and numerical patterns. The development of modular arithmetic is marked by its application in solving real-world problems related to calendars, timekeeping, and divisibility.
Carl Friedrich Gauss, a prominent mathematician, notably shaped the modern understanding of modular arithmetic. His seminal work, "Disquisitiones Arithmeticae," published in 1801, emphasized the arithmetic of remainders as a foundational aspect of this mathematical discipline. Today, modular arithmetic is an indispensable tool, seamlessly integrated into various branches of mathematics.
Beyond its historical significance, modular arithmetic emerges as a versatile tool with applications spanning cryptography, computer science, and beyond. Its distinctive arithmetic, centered around remainders, allows for the simplification of complex computations involving residual values. In subsequent sections, I will unravel the intricacies of modular arithmetic operations, exploring how it harmonizes with fundamental mathematical expressions involving addition, subtraction, multiplication, and division.
Modulus Properties
- ◈ If A ≡ B (mod C) then B ≡ A(mod C)
- ◈ If A ≡ B (mod C) and B ≡ D (mod C) then A ≡ D(mod C)
- ◈ (A + B) mod C = (A mod C + B mod C) mod C
- ◈ (A - B) mod C = (A mod C - B mod C) mod C
- ◈ (A * B) mod C = (A mod C * B mod C) mod C
- ◈ Aᴮ mod C = ( (A mod C)ᴮ ) mod C
Number Theory Applications
Explore practical applications of modular arithmetic in number theory, covering Fermat's Little Theorem, Euler's Totient Function, the Chinese Remainder Theorem, the Möbius Function, and the Divisor Sum Function. These applications showcase the versatility of modular arithmetic, from primality testing to cryptography.
01
Fermat's Little Theorem, a cornerstone of number theory rooted in modular arithmetic, states that if p is a prime number and a is an integer not divisible by p, then a*p−1≡1(mod p). This theorem provides a powerful tool for verifying primality and plays a crucial role in modular exponentiation.
02
Euler's Totient Function, denoted as ϕ(n), is intimately connected to modular arithmetic. It calculates the count of positive integers less than n that are coprime to n. Specifically, ϕ(n) is the order of the multiplicative group of integers modulo n, showcasing its inherent link to modular structures.
03
The Möbius function, denoted as μ(n), is a number-theoretic function deeply rooted in modular arithmetic. It is defined as follows: μ(n)=0 if n has a squared prime factor, μ(n)=1 if n is a product of an even number of distinct primes, and μ(n)=−1 if n is a product of an odd number of distinct primes.
04
The divisor sum function, often denoted as σ(n), involves the summation of all positive divisors of n. Its relationship with modular arithmetic becomes apparent when considering the properties of divisors in the context of modular operations, illustrating how modular arithmetic interfaces with divisor-related functions.
05
The Chinese Remainder Theorem efficiently solves systems of simultaneous modular congruences with pairwise coprime moduli. Ensuring a unique solution modulo the product of the moduli, it decomposes complex equations into simpler, independent components. This elegant theorem is fundamental in modular arithmetic, offering a concise method for handling intricate systems of equations.
Cryptography and Modular Arithmetic
Introduction
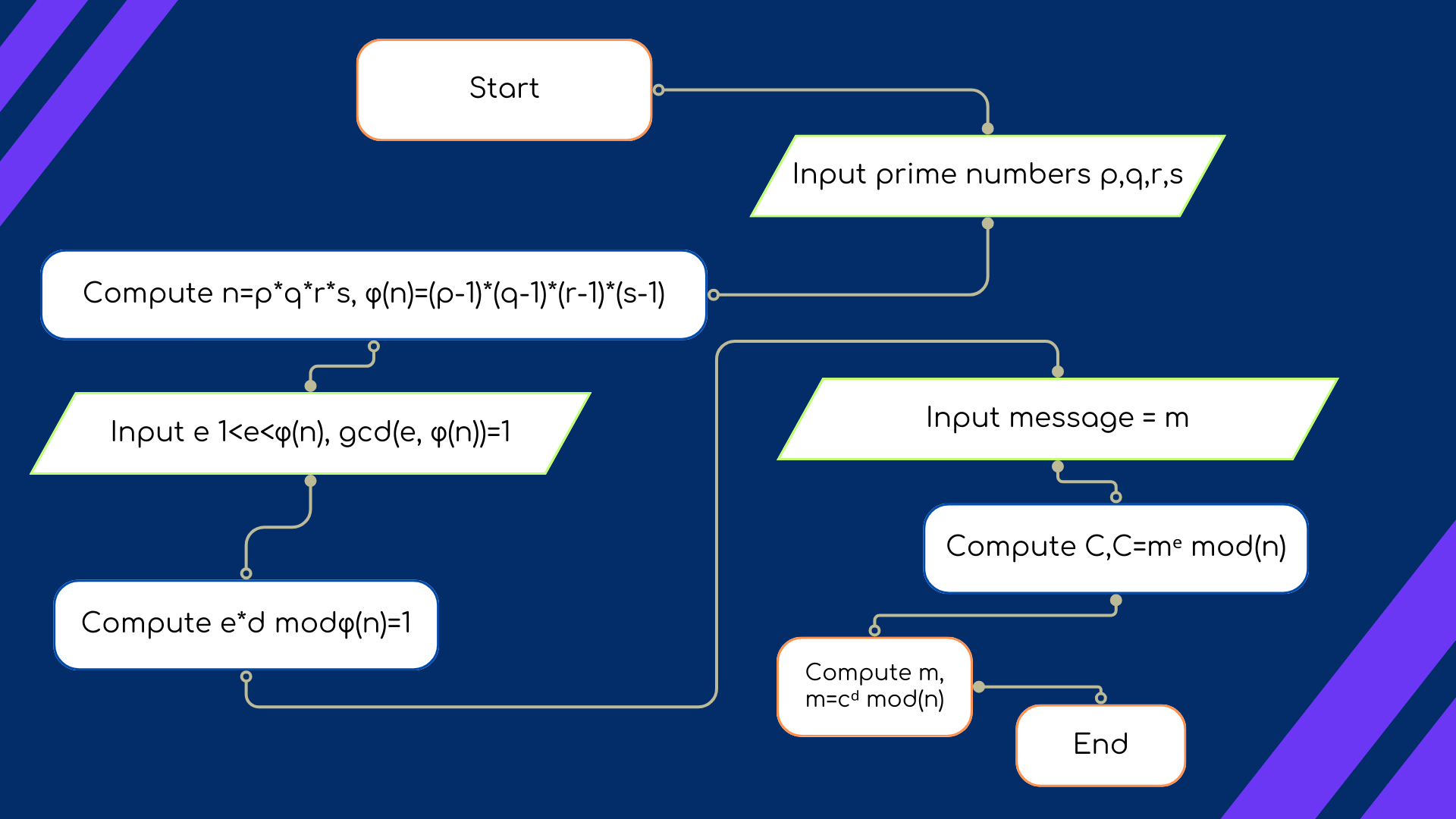
Cryptography, an essential aspect of secure communication, is deeply rooted in mathematical principles, with modular arithmetic serving as a cornerstone in various cryptographic algorithms. One such prominent algorithm is RSA, a widely used public-key cryptosystem known for its robust security features.
Modular Arithmetic in Cryptography:
1. Foundation of Cryptographic Operations:
◉ Modular arithmetic lays the foundation for cryptographic operations by introducing the concept of remainders when dividing integers.
2. RSA Algorithm Overview:
◉ RSA, a public-key cryptosystem, heavily relies on modular arithmetic for secure communication.
RSA Key Generation:
RSA key generation involves meticulous selection to ensure the security of the algorithm.
⊕ Public and Private Key Computation:
◉ The totient function φ(N) = (p-1)(q-1) is calculated.
◉ A public exponent 'e' is chosen, often a small prime.
◉ The private exponent 'd' is computed such that (e * d) ≡ 1 (mod φ(N)).
Modular Arithmetic in RSA Encryption:
1. Plaintext to Numerical Value:
◉ The plaintext is converted into a numerical value, M.
2. Encryption Process:
◉ Cipher text (C) is computed using modular exponentiation: C≡M*e (mod N).
3. Clarification in RSA Encryption:
◉ Encryption involves raising the plaintext M to the power of the public exponent e and then taking the result modulo N: C≡M*e (mod N).
RSA Algorithm and Modular Arithmetic
Detailing RSA Key Generation:
The RSA key generation involves the selection of two large prime numbers, p and q. The product N=p*q forms the modulus for both the public and private keys. Mathematically, this process is represented as:
N=p*q
The security of RSA relies on the complexity of factoring N. Larger prime numbers increase the difficulty of this factorization, thus enhancing security. The public key e and private key d are then computed using modular arithmetic:
e*d≡1(modϕ(N))
Here, ϕ(N) is Euler's totient function, and ≡ denotes congruence.
Clarification in RSA Encryption and Decryption:
RSA Encryption:
The encryption process involves raising the plaintext M to the power of the public exponent e and then taking the result modulo N:
C≡M*e(modN)
RSA Decryption:
Decryption uses the private exponent d to recover the original plaintext. The ciphertext C is raised to the power of d modulo N:
M≡C*d(modN)
Security and Applications of RSA:
RSA's security is deeply rooted in modular arithmetic, especially in the context of key length considerations and addressing challenges:
Key Length Considerations:
The length of N significantly impacts security. A longer N provides resistance against brute-force attacks.
Challenges Over Time:
Ongoing advancements in computing necessitate adjustments in key length to maintain security standards.
Vulnerabilities and Solutions:
Historical vulnerabilities, like insufficient randomness in key generation, have been addressed through continuous algorithmic evolution.
Linking Modular Exponentiation to RSA:
The core of RSA encryption and decryption lies in modular exponentiation.
For encryption:
C≡M*e(modN)
And for decryption:
M≡C*d(modN)
This integration with modular arithmetic ensures the security of RSA, creating a formidable mathematical foundation against unauthorized access and information compromise.
Examples
Introduction
Problem: If it's currently 3 o'clock, what time will it be in 14 hours using a 12-hour clock?
Solution: (3+14) mod 12=5.
So, it will be 5 o'clock.
Problem: If an event starts at 8:45 and lasts for 2 hours and 30 minutes, what time will it end?
Solution: (8×60+45+150)mod 720=375mod 720=375.
Converting 375 back to hours and minutes, the event will end at 6:15.
Problem: If today is Tuesday, what day will it be 10 days from now?
Solution: (2+10)mod 7=5.
So, it will be Sunday.
Problem: If today is Friday, and you want to know the day of the week 25 days from now, what day will it be?
Solution: (5+25)mod 7=2.
So, it will be a Tuesday.
Problem: Calculate (210)mod 7.
Solution: (210)mod 7 = 1024 mod 7 = 3.
Problem: Find the modular inverse of 9 modulo 26, denoted as 9−1mod 26.
Solution: 9×3≡1(mod26)
So, 9−1mod 26=3.
Problem: Solve the congruence 3x≡4(mod7).
Solution: x≡5(mod7)
Problem: Solve the system of simultaneous congruences:
x≡2(mod3) x≡3(mod5)
Solution: x≡8(mod15)
Problem: In a simplified cryptographic scenario, encrypt a message M=15 using a public exponent e=3 and a modulus N=35.
Solution: C≡ Mᵉ mod N=15³ mod 35=15.
Image gallery
Conclusion
In conclusion, this project has explored modular arithmetic as a fundamental concept and its crucial role in cryptography. The RSA algorithm served as a practical example, illustrating how modular arithmetic ensures secure communication through key processes.
This exploration highlights the essential nature of modular arithmetic in cryptography, emphasizing its role in securing digital information. The principles discussed lay a solid foundation for advancing and fortifying digital security practices.